The Bayes Classifier

The Bayes classifier is a Data Scientist's unbeatable arch enemy. When faced with the challenge of finding an optimal solution to a classification problem, it is the ultimate (theoretical!) benchmark when evaluating the performance of a classifier. The problem with the Bayes classifier is that it uses information that generally is not available to us in the real world. Therefore, it is more like a theoretical tool that shows that an optimal classifier always exists. Also, it shows us that given enough information about a problem, then a simple idea can lead to the optimal solution.

This blog post was inspired by exercise 7 of chapter 3.5 of the book Understanding Machine Learning. Since this blog post contains some hints for solving this exercise, it is a good idea to try and solve it yourself first. If you get stuck, feel free to return to this blog post.

Means and medians revisited

The Bayes classifier is related to the ordinary median; since we are about to find out why the Bayes classifier is always optimal (given that we precisely know the distribution of our data) let us first revise what optimization problem the median solves. Since the proof will be somewhat computation heavy, let us do the same for the mean first. This may be seen as an add-on to the blog post Means and medians where a general theme about these two invariants has already emerged: While both serve similar purposes, usages of the median in theoretical contexts are always more involved.

Theorem. Let \(X\) be a real valued random variable.

mean minimizes the \(L^2\)-distance to \(X\), i.e., it satisfies \[ \mathbb{E}[X] = \mathop{\mathrm{argmin}}_{c \in \mathbf{R}} \mathbb{E}\left[(X-c)^2\right]^{1/2}. \]
median minimizes the \(L^1\)-distance to \(X\), i.e., it satisfies \[ \mathbb{M}[X] = \mathop{\mathrm{argmin}}_{c \in \mathbf{R}} \mathbb{E}[|X-c|], \] where \(|\cdot|\) denotes the absolute value.

The theorem tells us that both the mean and the median are real numbers that are closest to the random variable; however, they are closest in different measures.

A short digress on different distance metrics

In case you are still wondering about what the different notions of distances are supposed to mean, the following should get you covered. There is an intrinsic need for different distance metrics: While a plane may travel the direct path from one point of the world to another, a car has to stick to roads and a train is bound to rails. So what exactly is a distance? Or, more precisely, what are the essential features of the different distance metrics that all of them share? This is where mathematicians get excited: Extracting similarities from a priori different entities and finding an appropriate abstraction that unites them is one of our main selling points. Here's what mathematicians have come up with a long time ago:

A distance metric is a function assigning a real value (the distance) to any two points in space such that

the distance from any point to itself is zero,
the distance from any point \(a\) to another \(b\) is the same as the distance from \(b\) to \(a\) (distances should be symmetric), and
the distance from any point \(a\) to another \(b\) is always smaller than or equal to the sum of the distances from \(a\) to yet another point \(c\) and from \(c\) to \(b\) (making roundabouts increases distance).

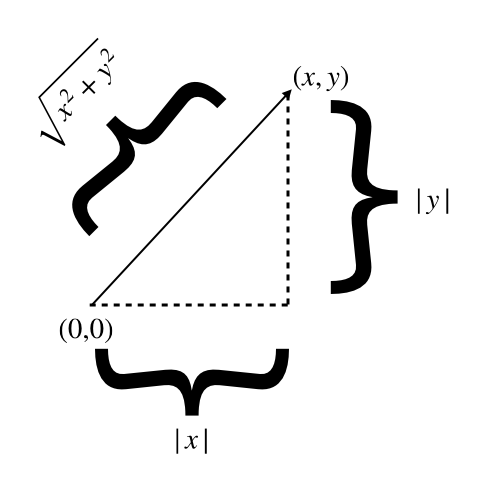
A related measure is length. Imagine a two dimensional coordinate system. If we use the usual picture of vectors as arrows in that coordinate system then we may assign a real value to each vector by measuring the length of that arrow. This yields the so-called euclidean norm or the \(2\)-norm. The formula for the length of the vector pointing from the origin to the point \((x,y)\) is \(\|(x,y)\|_2 := \sqrt{x^2 + y^2}\). We obtain a distance metric when postulating that this length is the distance from the point \((x,y)\) to the origin \((0,0)\). There are many other kinds of lengths; one of many examples is the \(1\)-norm defined by \(\|(x,y)\|_1 := |x| + |y|\). The distance metric induced by this norm is the distance when you are only allowed to move horizontally or vertically across two dimensional space. /images/bayes_distances.png

Let us turn to (discrete) random variables and how to make sense of the \(L^1\)- and \(L^2\)-distances. As you might suspect by now, they are related to the \(1\)- and \(2\)-norms, respectively. Let us assume that we are given a random variable \(X\) attaining two values \(x\) and \(y\). Let the probability that \(X = x\) be \(p\) so that \(P(X=y) = 1-p\). By the explicit formula for the mean, we see \[ \mathbb{E}[|X|] = p|x| + (1-p)|y| = \|(px, (1-p)y\|_1\] and, likewise, \[ \mathbb{E}[X^2]^{1/2} = \sqrt{px^2 + (1-p)y^2} = \|(\sqrt{p}x, \sqrt{1-p}y)\|_2.\] This means that the \(L^1\)-distance is a probability-weighted version of the \(1\)-norm, while the same holds for the \(L^2\)-distance and the \(2\)-norm. This might explain why the mean is simpler to use in theoretical contexts or why it might feel more natural (especially given its simple definition): It comes from minimizing a distance metric induced by the natural euclidean distance.

The proof

For the mean

Let us tackle the mean first. There is a pretty straightforward proof that uses calculus: First notice that because the square root is a monotonic increasing function, is suffices to show that the mean minimizes \(c \mapsto \mathbb{E}\left[(X-c)^2\right]\). Then, by linearity of the expected value, this is a quadratic polynomial in \(c\) so that it attains precisely one minimum. By calculus, computing that minimum is now just a matter of taking the derivative and solving a linear equation. However, I want to give you one proof that does not even need calculus. We merely need to use an equation that you might know as the third binomial formula: \(a^2 - b^2 = (a+b)(a-b)\). Here's how it goes. Getting rid of the square root is done by the same argument as before. Then, for any two real values \(c\) and \(d\), we compute \[ \begin{align*} \mathbb{E}[(X-c)^2] - \mathbb{E}[(X-d)^2] &= \mathbb{E}[(X-c)^2 - (X-d)^2] \\ &= \mathbb{E}[(X-c + X-d)(X-c-X+d)] \\ &= \mathbb{E}[(2X-c-d)(d-c)] \\ &= (2\mathbb{E}[X]-c-d)(d-c). \end{align*} \] Here, we have used linearity of the expected value in the first step, the third binomial formula with \(a = X-c\) and \(b = X-d\) in the second and linearity of the expected value in the last as well as the fact that the expected value of a constant random variable (such as \(c\) and \(d\)) equals that constant. This chain of equations holds for any two real values. This means it particularly holds for \(d = \mathbb{E}[X]\). Let's plug this in: \[\begin{align*} \mathbb{E}[(X-c)^2] - \mathbb{E}[(X-\mathbb{E}[X])^2] &= (2\mathbb{E}[X]-c-\mathbb{E}[X])(\mathbb{E}[X]-c) \\ &= (\mathbb{E}[X]-c)^2 \geq 0, \end{align*}\] as the square of any real number is non-negative. Reformulating, this means \[ \mathbb{E}[(X-c)^2] \geq \mathbb{E}[(X-\mathbb{E}[X])^2] \] holds for any real value \(c\) showing that \(\mathbb{E}[X]\) minimizes \(L^2\)-distance to \(X\).

For the median

While the idea for showing that the median minimizes \(L^1\)-distance is the same as in the proof above for the mean, be warned that this part is a lot more finicky. Because the absolute value is not differentiable, a straightforward proof using calculus is not available either. We will start like before by computing \(\mathbb{E}[|X-c|] - \mathbb{E}[|X-d|]\) for any two real values \(c\) and \(d\). One technicality I have to introduce to you is the so-called indicator function of a set \(A\) that I will denote by \(\chi_A\). This is a function that is \(1\) on \(A\) and \(0\) anywhere else. We will use it to deal with certain case distinctions in a concise way. For starters, let us assume \(d > c\) and compute \[\begin{align*} \|X-d\| - \|X-c\| &= \chi_{\{X \leq c\}}(\|X-d\| - \|X-c\|) + \chi_{\{X > c\}}(\|X-d\| - \|X-c\|) \\ &= \chi_{\{X \leq c\}}(d-X-c+X) + \chi_{\{X > c\}}(\|X-d\|- X + c) \\ &= \chi_{\{X \leq c\}}(d-c) + \chi_{\{d > X > c\}}(d-X - X + c) + \chi_{\{X \geq d\}}(X-d- X + c) \\ &= \chi_{\{X \leq c\}}(d-c) + \chi_{\{d > X > c\}}(d-2X + c) + \chi_{\{X \geq d\}}(-d+c) \\ &\geq \chi_{\{X \leq c\}}(d-c) + \chi_{\{d > X > c\}}(-d+c) + \chi_{\{X \geq d\}}(-d+c) \\ &= \chi_{\{X \leq c\}}(d-c) + \chi_{\{X > c\}}(-d+c). \end{align*}\] Here, we first split up the computation into the cases \(X \leq c\) and \(X > c\), getting rid of some of the absolute values. The next step was to split up the second case into the cases \(d > X > c\) and \(X \geq d\). Finally, in this second case we realized that we can estimate \(-2X > -2d\). After that, we simply united these two cases back together. Now, applying the expected value to this inequality and using monotony and linearity, we end up with \[\begin{align*} \mathbb{E}[|X-d|] - \mathbb{E}[|X-c|] &\geq \mathbb{E}[\chi_{\{X \leq c\}}](d-c) + \mathbb{E}[\chi_{\{X > c\}}](-d+c) \\ &= (d-c)\left(P(X \leq c) - P(X > c)\right) \\ &= (d-c)\left(2P(X \leq c) - 1\right) \end{align*}\] In the case \(d < c\), we may do a very similar computation by splitting up on \(X \geq c\) and \(X < c\). In this case, we end up with \[\mathbb{E}[|X-d|] - \mathbb{E}[|X-c|] \geq (c-d)\left(2P(X \geq c) - 1\right).\] What was this good for? If we plug in \(c = \mathbb{M}[X]\) in either case, we end up with \[\mathbb{E}[|X-d|] - \mathbb{E}[|X-\mathbb{M}[X]|] \geq 0\] as \(P(X \geq \mathbb{M}[X]) = P(X \leq \mathbb{M}[X]) = 1/2\). This shows that the median minimizes \(L^1\)-distance.

Classification problems

Let us use stochastics to model the following setup. We are given a bunch of data samples. Each data sample is either labeled (classified) as positive (1) or negative (0). Given an unlabeled data sample, we are tasked with giving a good estimate of whether it should be labeled as positive or negative.

An example

We are given news articles and are tasked with finding out whether they are about sports or not. In this case, our data samples consist of word count vectors generated from those articles (this means that for each article we create a table containing the information how often words appear in the article). Our positive data samples will be the sports articles.

Even for this simple example, we see that both the labeling as well as the information in the data sample are dependent of each other: For instance, an article containing sports-related words ('football', 'competition', …) is much more likely to be, in fact, a sports article while an article labeled as a sports article is much more likely to contain sports-related words more often than the average article.

Furthermore, this is a classical example of an inference pipeline. For data to become interpretable by a classifier, it has to be transformed appropriately first. In this case, the raw data might be given by the article, its headlines, and sub headlines. The raw data will then be transformed into a word count vector that in turn is fed into a classifier that predicts whether the article is about sports or not. /images/bayes_classifier_word_counts.png

Modelling classification problems

Since we do not know anything else about the problem, we might as well assume that the data samples are given to us at random, adhering to a probability distribution \(P\). More precisely, given a set \(S\) as our sample value space, we think of the data samples as an \(S\)-valued random variable \(X\) and of the labeling as a \(\{0,1\}\)-valued random variable \(Y\). In general, \(X\) and \(Y\) will very much depend on each other, as we saw in the preceding example: The values of \(X\) could be word count vectors while \(Y\) could be the labeling of the underlying article as being sports-related or not. We could model the bunch of data samples as a set; however, it is possible that there are duplicate data samples, even with the same label. Since we want to research on the underlying probability distribution, the occurrence of such duplicate data samples could carry precious information. Thus, we opt for modeling the given data samples as an element of \((S \times \{0,1\})^m\), with \(m\) being the amount of data samples obtained. Given such a tuple, we are tasked with constructing a classifier, i.e. a function \[f\colon S \to \{0,1\}.\]

Loss functions

How do we know if we have actually found a good classifier? What could good mean in this context? The idea of a loss function is to penalize each false prediction of the classifier. The penalty could be a constant number or it could depend on whether or positive or a negative sample has been falsely predicted. For this simple task at hand, the easiest would be to take the empirical risk.

Definition. Given an \(m\)-tuple of labeled data samples \(D\), the empirical risk of a classifier \(f\) is given by \[ L_{\mathrm{ER},D}(f) := \frac{|\{(x,y) \in D \mid f(x) \neq y \}|}{m}. \]

In other words, the empirical risk of a classifier computes the fraction of falsely predicted data samples. This means that the classifier is penalized by \(1/m\) for each false prediction. While this might be a good start for evaluating the performance of a classifier, concentrating on minimizing empirical risk alone is prone to overfitting, i.e. producing classifiers that perform well on the data samples obtained but fail miserably on new data.

What we should be more interested in, even though will not be computable in real world examples, is the true risk of a classifier.

Definition. If \(P\) is the probability distribution of the tuple of data samples and labelings \((X,Y)\), then the true risk of a classifier \(f\) is given by \[ L_P(f) := P(\{(x,y) \mid f(x) \neq y\}).\]

In other words, the true risk of a classifier penalizes false predictions of labeled data \((x,y)\) by the true probability of them occurring. In comparison, the empirical risk tries to approximate the true probability by the relative frequency of the labeled data sample in our sample set. If our sample set is large enough, this should be a good approximation; however, if we are out of luck, our sample set could contain labeled data samples with much higher frequency than they usually appear in the wildness. This leads to some interesting approaches of dealing with classification problems by minimizing the true risk for all probability distributions simultaneously. These approaches allow for a slim margin of error depending on the size of the sample set. But this is for another blog post.

The Bayes classifier

What would we do if we knew the underlying probability distribution \(P\)? Given an unlabeled data sample \(x \in S\), we could compute the probability of its label being positive \(P(Y = 1 \mid X = x)\). This is a conditional probability and may be read as the probability of \(Y\) being \(1\) given that \(X = x\). If this probability is bigger than \(1/2\) we should place our bet on the label being positive. Otherwise, it should be negative. This simple assignment is the Bayes classifier.

Definition. For the probability distribution \(P\) of \((X,Y)\), the Bayes classifier is the classifier given by \[ f_P\colon x \mapsto \begin{cases} 1 & P(Y=1 \mid X = x) \geq 1/2 \\ 0 & \text{else}\end{cases}.\]

An idea, no matter how simple, might yield a good result. In this case, in fact, the simple idea underlying the Bayes classifier yields the optimal result.

Theorem. The Bayes classifier minimizes the true risk. More precisely, given any other classifier \(f\colon S \to \{0,1\}\), the inequality \[ L_P(f) \geq L_P(f_P) \] holds.

Note that even though the Bayes classifier minimizes the true risk, its empirical risk could be arbitrarily high. Indeed: Consider a sample set consisting of one data sample that is labeled as positive. Assume that the probability of that data sample being labeled positively is smaller than \(1/2\). This one data sample is then mislabeled by the Bayes classifier yielding an empirical risk of \(1\).

The connection to the median

Before diving into the proof and to prepare for it, let me explain the connection between the Bayes classifier and the median of a random variable. In fact, the value \(f_P(x)\) for any unlabeled data sample \(x\) may be interpreted as the conditional median of the random variable \(Y\) given \(X = x\). Here's what this means: The value of the Bayes classifier satisfies \[\begin{align*} P(Y \geq f_P(x) \mid X = x) &\geq 1/2 \text{ and} \\ P(Y \leq f_P(x) \mid X = x) &\geq 1/2. \end{align*}\] Indeed, if \(f_P(x) = 1\) then \[P(Y \geq f_P(x) \mid X = x) = P(Y = 1 \mid X = x) \geq 1/2\] and \[P(Y \leq f_P(x) \mid X = x) = P(Y \in \{0,1\} \mid X = x) = 1 \geq 1/2.\] The proof for \(f_P(x) = 0\) is similar.

A sketch for the proof

As the proof for the Bayes classifier minimizing the true risk uses conditional expectations that I have not yet talked about, I will only give a sketch consisting of hints for the experts here. Also, this is the solution of exercise 7 in chapter 3.5 of Understanding Machine Learning; feel free to read this if you are stuck but I suggest on getting your hands dirty yourself first and giving this exercise a good try.

Ready? The first step is to rephrase the true risk as \[ L_P(f) = \mathbb{E}[|Y - f(X)|]. \] Then, we may use one of the central properties of conditional expectations: The expected value of a conditional expectation of a random variable is the same as the expected value of the random variable. This yields \[ L_P(f) = \mathbb{E}\left[\mathbb{E}[|Y - f(X)| \mid X]\right]. \] Now we are almost done. By monotony of the expected value, it suffices to minimize \(\mathbb{E}[|Y - f(X)| \mid X]\) pointwise. And this is precisely what the Bayes classifier does by the preceding paragraph: For each \(x \in S\), \(\mathbb{E}[|Y - f(x)| \mid X = x]\) is minimal if \(f(x)\) is the conditional median of \(Y\) given \(X = x\) which is the value \(f_P(x)\) of the Bayes classifier.